Simulation numérique de la propagation de fissures en utilisant la méthode des éléments finis avec Ansys.

Introduction :

Ansys Workbench™ est une plateforme de simulation complète, largement utilisée pour modéliser la croissance des fissures, qu'elles soient statiques ou induites par la fatigue. Elle offre des outils avancés et des capacités permettant d'analyser et de prédire avec précision le comportement de propagation des fissures sous des conditions de chargement statique et cyclique. Ansys est un logiciel puissant pour l'analyse par éléments finis.

Le langage de conception paramétrique Ansys est utilisé dans cet contribution pour calculer les facteurs d'intensité des contraintes (SIF), la direction de croissance des fissures, ainsi que la distribution des contraintes et des déformations pour différentes géométries.

En intégrant les principes de la mécanique de la rupture, les propriétés des matériaux et les techniques d'analyse de la fatigue, AnsysWorkbench permet aux ingénieurs et aux chercheurs d'acquérir des informations précieuses sur la durée de vie en fatigue et la durabilité des structures. L'intégration d'une technique de simulation incluant une analyse numérique et l'utilisation de la méthode des éléments finis avec Ansys Mechanical™ est un excellent moyen de réduire les efforts en laboratoire, le temps et les coûts.
Ansys Workbench propose une gamme de modèles de croissance de fissures, y compris la technique de fermeture virtuelle de fissure (VCCT), la méthode étendue des éléments finis (XFEM) et la modélisation de zone cohésive (CZM). Ces modèles permettent une représentation précise de la géométrie des fissures, la prise en compte de conditions de chargement complexes et la simulation de la propagation des fissures dans divers matériaux et structures.

Les différents types de fissures intégrés dans Ansys :

La génération de maillage est une étape critique qui influence la performance de l'analyse par éléments finis. Ansys Workbench fournit un générateur de maillage structurel fiable et robuste capable de générer un maillage cohérent pour toute la structure avec un effort de calcul minimal. Ansys peut modéliser trois types de fissures : semi-elliptique, arbitraire, et pré-maillé.

Les fissures semi-elliptiques sont définies par des paramètres géométriques précis comme la longueur et la largeur de l'ellipse, qui déterminent leur forme exacte. Le front de fissure, quant à lui, représente la ligne ou la courbe où la fissure commence à se propager dans le matériau. En ajustant ces paramètres dans le panneau de détails d’Ansys Workbench, il est possible de contrôler finement le maillage autour de la fissure pour assurer une précision maximale dans les simulations. La génération du maillage de fissure intervient après la création du maillage de base du modèle, automatisée par Ansys Workbench pour simplifier et accélérer la préparation du modèle pour l'analyse. En outre, Ansys crée automatiquement une sélection nommée des nœuds le long du front de fissure.

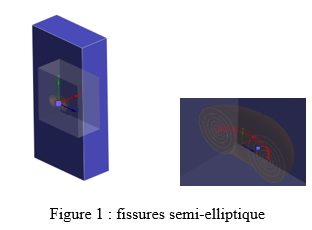
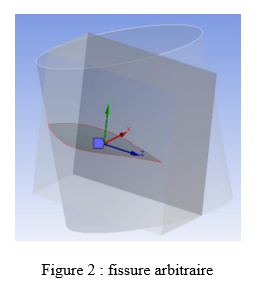
Les objets de fissure arbitraires dans Ansys sont utilisés pour modéliser des fissures de formes variées dans des analyses tridimensionnelles. Pour définir la forme de la fissure, on sélectionne un corps de surface dont les bords extérieurs servent à délimiter le front de la fissure. La surface elle-même définit le plan de la fissure, marquant la discontinuité dans le matériau.

Lors de la simulation, Ansys génère d'abord le maillage de base du modèle, puis procède à la génération du maillage spécifique à la fissure. Par défaut, Ansys crée automatiquement une sélection nommée basée sur les nœuds pour le front de fissure sous l'objet de fissure arbitraire.

Un crack pré-maillé dans Ansys repose sur un maillage déjà existant, souvent importé d’une source externe ou créée manuellement. Cette méthode est idéale pour modéliser des fissures préconçues en CAO ou utiliser un maillage généré en dehors d'Ansys. L'analyse de la fissure se concentre sur les nœuds le long du front de fissure, définis via une sélection nommée basée sur les nœuds.

ANSYS SMART Crack Growth :

La nouvelle technologie de Séparation, Morphing, Adaptation et Remeshing (SMART) représente une avancée majeure d'Ansys pour relever les défis critiques liés à l'initiation, à la croissance et à la rupture des fissures dans la conception de produits.

Comprendre la sécurité, la fiabilité et la durabilité des composants et des structures est essentiel. Traditionnellement, les ingénieurs ont utilisé des prototypes physiques et des tests pour évaluer la résistance à la rupture. Cependant, Ansys propose désormais un logiciel de simulation de haute qualité qui permet aux ingénieurs de prédire la résistance à la rupture de manière plus efficace que jamais. En effet, une avancée significative réside dans l'intégration de la méthode de maillage non structuré (UMM) à l'algorithme SMART d'Ansys, ce qui se traduit par une réduction considérable du temps de prétraitement. À chaque étape de la résolution, SMART ajuste automatiquement le maillage pour refléter les évolutions géométriques de la fissure dues à sa croissance. En générant un maillage tétraédrique automatique pour les fronts de fissure, cette méthode permet aux ingénieurs d'obtenir des résultats haute-fidélité tout en réduisant le temps de maillage de plusieurs jours à quelques minutes.

SMART utilise une méthode de remaillage localisé au lieu de recourir à la technique d'enrichissement pour suivre le développement de la fissure. Contrairement à la méthode XFEM, cette approche permet à SMART de s'adapter à des projets de plus grande envergure en se concentrant sur une petite zone autour de la pointe de la fissure à chaque itération de remaillage. Cette optimisation ciblée des ressources de calcul là où elles sont le plus nécessaires améliore la vitesse des simulations SMART et les rend plus facilement adaptables à des projets complexes. De plus, cette méthode n'exige pas le développement de nouveaux éléments et permet d'utiliser les éléments conventionnels intégrés dans Ansys Mechanical.

ANSYS SMART Crack Growth représente une avancée significative dans la modélisation de la croissance des fissures par fatigue. Traditionnellement, cette analyse nécessitait des tests physiques intensifs, coûteux et chronophages. Toutefois, avec les progrès des techniques de simulation numérique, les ingénieurs et chercheurs disposent maintenant d'un outil puissant pour prédire et analyser le comportement des fissures de manière plus efficace et économique. Intégrant une approche basée sur un maillage tétraédrique, Ansys simplifie le processus de modélisation de la croissance intelligente des fissures. Cette fonctionnalité prend en charge plusieurs fronts de fissure, permettant l'analyse de structures complexes. Elle offre également la flexibilité d'analyser à la fois la croissance de fissures statiques à l'aide d'intégrales de J et de facteurs d'intensité de contrainte ( SIFs ), ainsi que la croissance de fissures par fatigue avec des lois dédiées comme la Loi de Paris.

Vérification de calcul de Facteur d’intensité de contrainte pour un exemple 2D

Dans la question présente, nous considérons une plaque comme étant rectangulaire, avec des dimensions (Fig .). Le maillage a été généré par le programme Ansys (Pre_meched crack). La plaque était en acier avec un module d'élasticité E=200 GPa et un coefficient de Poisson ν=0.3. Une contrainte de traction uniforme σ =150 MPa a été appliquée aux deux surfaces (Fig. a).

Le code des éléments finis Ansys a été utilisé pour vérifier les différents facteurs d'intensité de contrainte (SIF).

Le facteur d'intensité de contrainte analytique K_I pour ce problème est donné par [ ] comme suit :

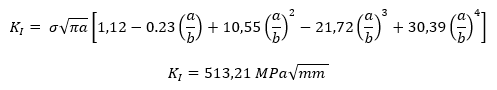
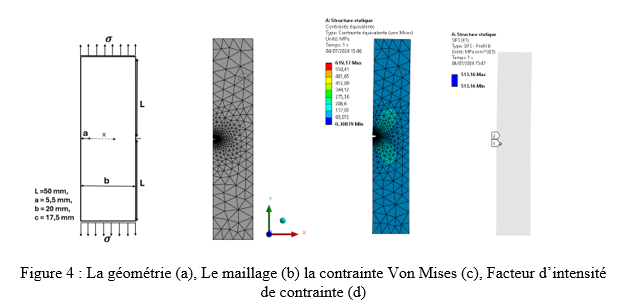
On peut constater que les résultats obtenus sont très proportionnels et acceptables.

Une plaque fissurée avec quatre trous

Dans cet exemple, le chemin de croissance de la fissure est dévié en raison de la présence de plusieurs trous dans une forme relativement compliquée. Une plaque carrée contenant quatre trous de rayons égaux de 5 mm et une fissure de bord de 6 mm de long est considérée, comme montré dans la Figure . La plaque mesure 100 mm × 100 mm × 10 mm. Une contrainte uniformément distribuée de σ = 10 MPa est appliquée le long des bords supérieur et inférieur de la plaque. Le matériau utilisé est l’acier avec les propriétés suivantes :

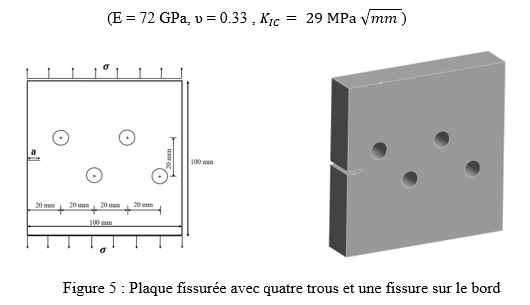
Dans cet exemple l'approche de fissure pré-maillée qui nécessite l'utilisation d'un front de fissure tel qu'identifié par l'outil d'analyse de croissance de fissure Smart a été utilisé. À chaque étape de la solution, SMART met automatiquement à jour le maillage en fonction des changements de géométrie de la fissure dus à sa propagation.

Le maillage de la pointe de la fissure et le bord géométrique qui traverse l'épaisseur ont été affinés en utilisant la sphère d'influence. La pointe de la fissure, la surface supérieure de la fissure et la surface inférieure de la fissure sont toutes incluses dans les régions géométriques. Chacune de ces régions est connectée à un ensemble de nœuds qui seront utilisés pour la simulation.

Pour la simulation de la croissance statique des fissures , Ansys Mechanical propose deux critères de fracture courants : l'intégrale J et le facteur d'intensité des contraintes. Dans cet exemple, le critère du facteur d'intensité des contraintes a été utilisé, lequel stipule que la fissure se propage lorsque le facteur d'intensité des contraintes équivalent dépasse la ténacité à la rupture du matériau. Ce calcul est effectué le long du front de fissure distribué, où la distribution du facteur d'intensité des contraintes contrôle la forme adaptative du front de fissure.

Le facteur d'intensité des contraintes équivalent est représenté dans la littérature [ ] comme suit :

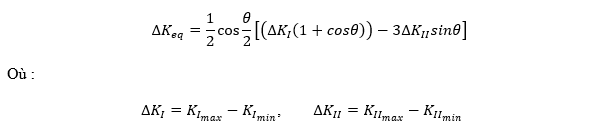
La direction de la propagation de la fissure est identifiée par un angle déterminé à partir du plan de fissure d'origine [ ]. Le rapport des modes de facteur d'intensité des contraintes à la pointe de la fissure détermine la direction d'une fissure en mode mixte.

Le critère de contrainte circonférentielle maximale est implémenté dans le logiciel Ansys pour le chargement en mode mixte. La formule pour la direction de la propagation de la fissure dans Ansys est exprimée comme suit [ ] :

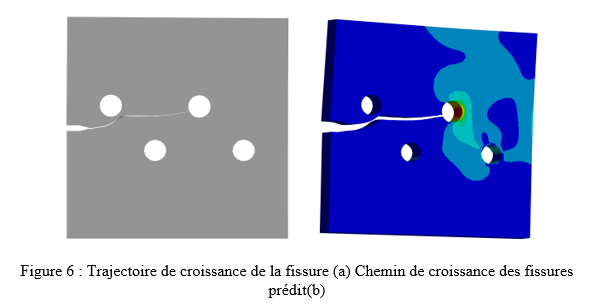
La Figure montre le trajet de propagation de la fissure, la fissure commence à se propager en ligne droite car il n'y a pas d'influence des trous. À mesure qu'elle s'approche du trou, elle se dirige vers le premier trou supérieur, qui n'était pas suffisamment proche pour que la fissure se dirige vers le trou ; par conséquent, la fissure a changé de direction et continue de se propager en ligne droite jusqu'à ce qu'elle arrive près du second trou supérieur, qui est suffisamment proche de la trajectoire de la fissure pour que celle-ci se dirige vers le trou. La présence d'un trou près d'une fissure en propagation peut entraîner des déviations dans le chemin de la fissure. Si le trou est suffisamment proche du chemin de la fissure, la fissure peut s'arrêter au bord du trou, entraînant un arrêt de la fissure.

Sous les principes de la mécanique de la rupture élastique linéaire (LEFM), le critère de contrainte circonférentielle maximale a été appliqué comme critère directionnel. Selon la position du trou, les résultats indiquent que la fissure a tendance à se propager vers le trou en raison des contraintes inégales à la pointe de la fissure induites par la présence du trou.

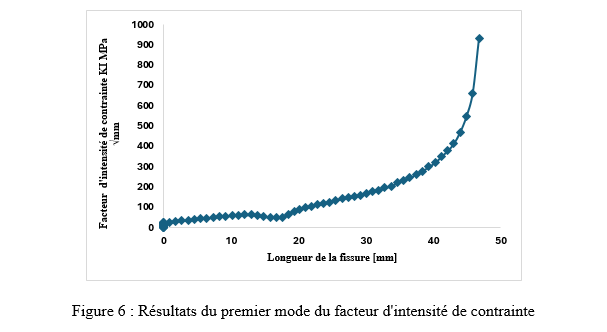
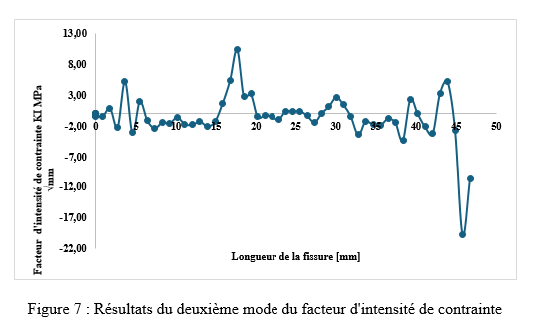
Les Figures 6 et 7 montrent les résultats des facteurs d'intensité des contraintes en mode mixte K_I,K_II. La trajectoire de croissance de la fissure a été représentée avec précision par ces valeurs estimées. En raison de l'influence du premier trou supérieur, les valeurs de K_I ont diminué dans l'intervalle de longueur de fissure compris entre 15 mm et 20 mm.

En revanche, le second mode du facteur d'intensité des contraintes a légèrement augmenté au cours de la même période, comme le montre la Figure 7. Par la suite, la valeur de K_I a recommencé à augmenter lorsque la trajectoire de la fissure a évité le premier trou supérieur jusqu'à ce que la fissure atteigne le second trou supérieur.